How Do Families Adapt to Social Changes and Economic Development
Abstract
Families class the basis of society, and anthropologists have observed and characterised a wide range of family systems. This study developed a multi-level evolutionary model of pre-industrial agricultural societies to simulate the evolution of family systems and determine how each of them adapts to environmental conditions and forms a characteristic socio-economic structure. In the model, competing societies evolve, which themselves comprise multiple evolving families that grow through family unit labour. Each family has two strategy parameters: the time children leave the parental home and the distribution of inheritance among siblings. The evolution of these parameters demonstrates that four bones family systems emerge; families can become either nuclear or extended, and have either an equal or strongly biased inheritance distribution. Nuclear families in which children get out the parental home upon union emerge where land resources are sufficient, whereas extended families in which children staying at the parental domicile sally where land resources are limited. Equal inheritance emerges where the corporeality of wealth required for a family to survive is big, whereas strongly biased inheritance emerges where the required wealth is small. Furthermore, the frequency of polygyny is depression in the nowadays model of agricultural societies, whereas it increases for the model of labour-all-encompassing subsistence patterns other than agricultural societies. Analyses on the wealth distribution of families demonstrate a higher level of poverty amidst people in extended families, and that the accumulation of wealth is accelerated in families with strongly biased inheritance. Past comparison wealth distributions in the model with historical information, family systems are associated with characteristic economical structures and then, modern social ideologies. Empirical information analyses using the cross-cultural ethnographic database verify the theoretical relationship between the ecology weather, family systems, and socio-economic structures discussed in the model. The theoretical studies fabricated possible by this simple effective model, equally presented here, will integrate the understandings of family systems in evolutionary anthropology, demography, and socioeconomic histories.
Introduction
Families are bones components of society. Studies of family and kinship lay at the core of anthropology (Pull a fast one on, 1983; Harrell, 1997; Lévi-Strauss, 1958; Shenk and Mattison, 2011). Families comprise people who are continued by three bones relationships, i.e. married man–married woman, parent–child, and inter-sibling relationships (White, 1963), and a variety of rules (or patterns) are observed concerning them (Harrell, 1997; Laslett, 1988; Todd, 1999). Cultural traits pertaining to family unit relationships are irksome to modify, considering they tend to be inherited vertically from parent to child, and are regulated by social norms (Cavalli-Sforza and Feldman, 1981). Indeed, empirical studies have revealed such slow changes based on population history (Guglielmino et al., 1995; Minocher et al., 2019; Mulder et al., 2001). Family traits have also attracted significant attention every bit relatively stable basic factors of social characteristics in the report of history (Braudel, 1992a, b, c) and historical demography (Macfarlane, 2002), amongst others.
The appearance of these traits was previously explained by cultural transmission or accommodation to social and ecological conditions (Goldschmidt and Kunkel, 1971; Laslett, 2015; Todd, 2011). Social studies unveiled a correlation betwixt the period of exposure to the Western Church and the emergence of nuclear families (Schulz et al., 2019). In evolutionary anthropology, relationships betwixt family members are explained based on parental investment theory and intra-family competition for reproductive resource (Ji et al., 2014; Trivers, 1974). Subsistence patterns and other socio-ecological conditions that affect family traits accept recently been revealed quantitatively (Colleran, 2014; Gibson and Gurmu, 2011; Macfarlan et al., 2019; Ross et al., 2018). Phylogenetic comparative analyses take been performed to infer the origin and historical change of family traits by controlling the statistical non-independence due to the shared ancestry (Fortunato and Jordan, 2010; Fortunato et al., 2006; Holden and Mace, 2003; Minocher et al., 2019; Mulder et al., 2001). In particular, they revealed that the presence of heritable resource that are typically observed in agricultural/ pastoralist social club leads to sibling contest over inheritance (Gibson and Gurmu, 2011) and to patriliny (Holden and Mace, 2003). Differentiation of very rich aristocracy from the majority in agricultural society leads to a lower frequency of polygyny (Ross et al., 2018).
Indeed, correlations have been observed between family traits and several socio-ecological atmospheric condition. However, it is unclear whether social factors determine family traits or vice versa (Mace and Hashemite kingdom of jordan, 2011). The reverse effect from family traits to social conditions is as well reported in historical census (Macfarlane, 2002).
As two characteristics in the family system, we consider parent–child and inter-sibling relationships. Although a variety of characteristics can represent these relationships, nosotros focus on residence and inheritance patterns. The residence pattern can refer to nuclear families that comprise a pair of parents and their single children, or to extended families that tin can involve parents and their married children. The inheritance pattern can refer to either the equal or strongly biased distribution of inheritance amidst siblings. On this ground, we tin can suppose 4 platonic types. (i) Absolute nuclear families, which are nuclear families with unequal inheritance. (2) Egalitarian nuclear families, which are nuclear families with equal inheritance. (3) Stem families, which are extended families with unequal inheritance. (4) Community families, which are extended families with equal inheritance. Indeed, other characteristics of family systems, such as marriage patterns, would be necessary to classify family systems comprehensively, which needs future works. Nevertheless, at that place is notable variation in the residence and inheritance patterns in pre-industrial agricultural societies in Europe, Northern Africa, and Asia, among others (Harrell, 1997). The influence of agricultural societies on political systems in the modernising era has been described (Rösener, 1993; Wallerstein, 2011). The link betwixt the above four family systems and mod social ideologies has been discussed (Laslett, 1988); Liberalism, liberal egalitarianism, social democracy, and communism are dominant in regions with accented nuclear, egalitarian nuclear, stem, and community families, respectively (Todd, 1990, 1999). However, the discussion regarding the relationship between family unit systems and ideologies remains largely psychoanalytical. Hence, theoretical studies to unveil the weather of the evolution of each family system and to connect family systems with socio-economic structures demand to be conducted.
To consider the interaction of ecological conditions, family systems, and social structures, a effective approach to reveal the relationships between them is required. In addition, given that family traits are inherited from parents with slight changes over generations, it is appropriate to model their long-term evolution through the aggregating of small variations, as represented by mutations. Past modelling the evolution of family systems to adapt to socio-ecological conditions, which in turn grade the society-level economic structure, we aim to integrate the understandings in evolutionary anthropology, demography, and socioeconomic histories. To model the economical consequence of family unit behaviour, nosotros focus on agricultural gild, where family unit systems determine residence and inheritance patterns in land usage (Todd, 1990, 2011). Children may cultivate lands of their own or piece of work together on their parents' land. One heir may inherit the land and most of the holding exclusively, or the state and property may be divided equally among family members (Berkner, 1976; Kaser, 2002). Characteristics of the pre-industrial agricultural guild include the importance of human labour, land and holding in production (Colleran, 2014), a positive correlation of wealth and the number of offspring (Gibson and Gurmu, 2011), and the diminishing returns to labour input (Evenson and Mwabu, 2001; Ricardo, 1891). Hereby, nosotros build the minimal model that is appropriate as long as these conditions are satisfied.
Notably, families constitute society, whereas society, too as environmental, provides the environment for families. Hence, our model adopts a framework involving multi-level evolution for a hierarchical organization. The multi-level development was originally introduced to explain the evolution of cooperative behaviour amongst eusocial insects by examining the disharmonize between the fitness of an individual and that of a group (Wilson, 1997; Wilson and Wilson, 2007). This framework is generally practical to the evolution of group-level structure in hierarchical systems (Spencer and Redmond, 2001; Takeuchi et al., 2017; Traulsen and Nowak, 2006; Turchin and Gavrilets, 2009). In the previous study, the framework was practical to construct a mathematical model for the evolution of kinship structures in clan societies, which revealed the environmental dependencies of diverse kinship structures (Itao and Kaneko, 2020, 2021a). The variety of family traits regarding cousin marriage preferences and association exogamy, besides as descent systems, were investigated in item therein. Here, in contrast, nosotros mainly focus on parent–child residence patterns and inter-sibling inheritance patterns, and briefly mention the conditions for polygyny.
In this study, we investigate the development of family unit systems and social structures by introducing an amanuensis-based multi-level evolutionary model of pre-industrial agronomical societies. Competition is considered at two levels: that of family, which is an private agent of the model, and gild, which is a grouping of families. Families produce wealth through family labour and reproduce their population. They possess ii strategy parameters concerning the time children leave their parents' home and the distribution of inheritance among them. These parameters are transmitted with slight mutations in each generation. Evolutionary simulations show that four family systems emerge depending on ecology parameters that characterise the land scarcity and perturbations that harm guild. Then, the model is extended by adding the marriage procedure. We show that this extension affects the above consequence only minimally, whereas it facilitates the discussion of atmospheric condition for son-biased investment and polygyny. Nosotros then describe the characteristics of social structure in terms of the distribution of wealth in lodge and chronicle them to family systems.
Finally, the theoretical results are verified through a data assay using the standard cantankerous-cultural sample (SCCS), a global ethnographic database of premodern societies (Kirby et al., 2016; Murdock and White, 1969). SCCS contains data from 186 societies, which are thought to be culturally and linguistically independent of each other. In the discussion section, we show the relationships between family unit systems, socioeconomic structures, and the development of political ideology in the modernising era, by referring to socioeconomic histories.
Model
Overview of the model
The model is described below in general terms in this subsection (see the following subsection for the mathematical formulation). A schematic of the model is shown in Fig. 1a, b. Society consists of families. In each family unit, private members live and work together. Children build families of their own by inheriting their parents' wealth. Wealth w is accumulated through production, which in plough increases the level of production and the population, as empirically reported (Gibson and Gurmu, 2011; Macfarlane, 2002). Each society splits into 2 when the number of families therein doubles its initial value Due north f, and each family is randomly assigned to one of the two daughter societies. At this time, some other society is removed at random so that the number of societies in the entire system remains fixed to North southward . This process can be interpreted as invasion, imitation, or the fibroid-grained clarification of a growing system. Therefore, societies that grow faster supersede others, resulting in club-level evolution. This multi-level evolution of families and societies follows the hierarchical Moran process (Itao and Kaneko, 2020; Takeuchi et al., 2017; Traulsen and Nowak, 2006).
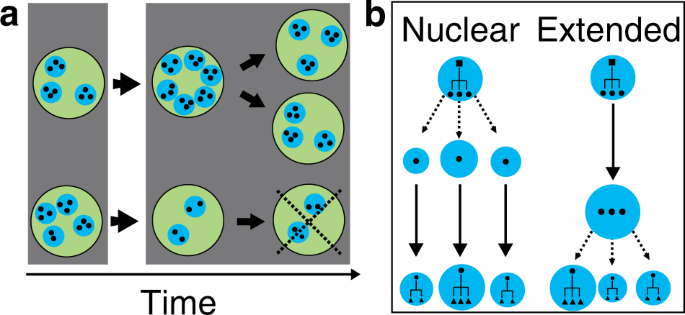
a The multi-level evolutionary process. Societies (greenish) comprise families (blue) in which family members (blackness) alive together. The grey frame represents a single generation. When the population of a society reaches twice the initial population, a guild splits and another society is removed from the system at random to keep the number of societies fixed—i.e. nosotros adopt the hierarchical Moran process. b The life bicycle of families. The black squares, circles, and triangles stand for members of dissimilar generations. The size of the blue circle reflects the amount of wealth that each family possesses. The dashed arrows show the separation of siblings, and the arrows show the product of wealth through family labour. Each family has a strategy parameter due south. With the probability of i−due south, siblings are separated before product, and then they produce independently and reproduce the side by side generation, as in a nuclear family. On the other hand, with the probability of due south, siblings produce together, later which they build their ain home and reproduce the next generation, as in an extended family. When we extend the model to consider union, its process is added just before production.
In each simulation, the environmental parameters are given. Of particular importance are the following two: the capacity c ×N f, which represents the corporeality of available land resource in society (hereafter called land capacity), and ϵ, which is wealth required for a family to survive the perturbations that damage society (future called wealth required for survival). Agronomical production depends on the amount of available country resources, whereas insufficient capacity limits state resources per family. In this model, when the number of families in a society exceeds the chapters, the land resources and the production rate for each family decrease inversely with the number of families at that time. As for the wealth required for survival, ϵ must exist paid by a family at the moment of its building. If wealth due west is less than ϵ, its members dice without reproducing.
Families have population and wealth, as well equally the ii strategy parameters, i.due east. λ, which represents the inequality in the inheritance of wealth among siblings, and due south, which represents the probability of children staying at their parents' habitation to produce together. The thouthursday child'due south share of the inheritance is proportional to \(\exp (-\lambda m)\). Therefore, λ = 0 represents an equal division of inheritance, whereas a larger λ represents the eldest child inheriting more. In some societies, the youngest child inherits the about instead of the eldest (Todd, 2011). If necessary, the order of children could be bundled in reverse to include such a case. Each family forms an extended family with probability s or otherwise forms a nuclear family unit (explained in item beneath). These parameters may exist adamant by intra-family contest amongst parents and siblings (Ji et al., 2014; Trivers, 1974). Hither, we practice not model the competition explicitly but do then implicitly by tracing the evolution of λ and s.
The life cycle of the families depends on the strategy due south. With the probability of 1−due south, siblings are separated before agronomical production, i.east. they inherit some property adamant by λ, lose ϵ of wealth, and build families of their ain to produce independently. In contrast, with a probability of s, siblings remain in their parents' family unit to produce together, after which they are separated. According to the law of diminishing returns, productivity increases sub-linearly with labour forcefulness input (Bacci, 2017; Malthus, 1798; Ricardo, 1891). Following a study on pre-industrial farming (Evenson and Mwabu, 2001), we assume that production increases in proportion to the logarithm of labour input, and is perturbed by Gaussian dissonance with a mean of 0 and a variance of σ 2, resulting from internal and environmental fluctuations.
Then, equally long as the law of diminishing returns is satisfied, the total output of siblings is always higher when each sibling produces independently to course a nuclear family unit than when they concentrate their labour in an extended family. In this model, the productivities of N members are \(Northward{{\mathrm{log}}}\,two\) and \({{\mathrm{log}}}\,(N+1)\) for nuclear and extended families, respectively. However, under a express capacity of available land resources, the total output of the society consisting of nuclear families volition be lower than that of extended families, as a result of inefficient land usage (the productivities are \(\frac{1}{Northward}N{{\mathrm{log}}}\,2\) and \({{\mathrm{log}}}\,(N+1)\) for nuclear and extended families, respectively). In other words, there is a disharmonize between family- and gild-level preferences for nuclear versus extended families under the atmospheric condition of limited chapters. As long as one considers pre-industrial farming, information technology is expected that family members work together on their land, and the police force of diminishing returns is satisfied. However, this formulation volition be inappropriate for modern farming or other subsistence patterns, which is beyond the scope of this model. The results for unlike formulations of labour-extensive subsistence patterns are briefly discussed.
After sibling separation and the product of wealth, each family reproduces. The number of children in families is positively correlated with their wealth in pre-industrial societies (Gibson and Gurmu, 2011). Here, we assume that it follows the Poisson distribution with a mean of b +f w, where b and f stand for the minimal nativity rate and the increment of birth rate by wealth westward, respectively. Children culturally inherit s and λ from their parents, with a slight variation through 'mutation' at the rate of μ, according to previous studies on cultural development (Cavalli-Sforza and Feldman, 1981; Creanza et al., 2017). At the fourth dimension of altering generations, families lose d due west of wealth, where d represents the decay rate of wealth due to ageing equipment, disaster, or taxation, for instance. Additionally, each society splits if the number of families reaches 2N f at that time. The parameters are summarised in Table 1.
The higher up is a minimal model to discuss the diversification of family systems concerning parent–child and inter-sibling relationships. To consider hubby–married woman relationships, we extend the model by assigning each family male and female populations, and the strategy for inheritance distribution for sons and daughters. In the extended model, i can have multiple spouses by paying sufficient bridewealth. Polygyny increases both production and reproduction. This model is explained in the Supplementary Text in detail.
Algorithm of the model
In this subsection, we show the mathematical formulation of our model. Nosotros adopted the post-obit algorithm for changes in the wealth and population of families. For the parent family unit i and its jthursday child'southward family i,j, the population Due north and the amount of wealth w at time t are expressed every bit follows:
$${westward}_{i}^{t* }=(1-d){w}_{i}^{t-one}.$$
(i)
With probability \(i-{s}_{i}^{t}\),
$${N}_{i,j}^{t}=1\ (one\le j\le {North}_{i}^{t}),$$
(two)
$${west}_{i,j}^{t* }={due west}_{i}^{t* }{due east}^{-{\lambda }_{i}^{t}j}/\mathop{\sum }\limits_{grand=1}^{{North}_{i}^{t}}{e}^{-{\lambda }_{i}^{t}k}-\epsilon ,$$
(3)
$${westward}_{i,j}^{t}={due west}_{i,j}^{t* }+r(1+\eta )(one+{w}_{i,j}^{t* }){{\mathrm{log}}}\,(1+{N}_{i,j}^{t});$$
(4)
otherwise,
$${due west}_{i}^{t}={w}_{i}^{t* }+r(i+\eta )(1+{w}_{i}^{t* }){{\mathrm{log}}}\,(one+{N}_{i}^{t}),$$
(v)
$${due west}_{i,j}^{t}={w}_{i}^{t}{due east}^{-{\lambda }_{i}^{t}j}/\mathop{\sum }\limits_{m=1}^{{Northward}_{i}^{t}}{eastward}^{-{\lambda }_{i}^{t}k}-\epsilon \,\,(1\le j\le {N}_{i}^{t}).$$
(vi)
Then,
$${N}_{i,j}^{t+1}=\,{{\mbox{Poisson}}}\,(b+f{west}_{i,j}^{t}),$$
(7)
$${s}_{i,j}^{t+1}={south}_{i}^{t}+\zeta ,\,\,{\lambda }_{i,j}^{t}={\lambda }_{i}^{t}+\zeta ,$$
(8)
where
$$r=\min (1,c{N}_{{\mathrm {f}}}/\#\,{{\mbox{families}}}\,),$$
(9)
$$\eta \sim N(0,{\sigma }^{two}),\,\,\zeta \sim N(0,{\mu }^{ii}).$$
(10)
In each simulation step (generation), families lose a proportion d of their wealth (Eq. (i)). With probability 1−s, siblings go out their parents' dwelling house (Eq. (2)), distribute the inheritance with a wealth loss of ϵ (Eq. (3)), and produce independently (Eq. (iv)). Otherwise (with probability due south), siblings produce together at their parents' home (Eq. (half dozen)) and build their own families afterward production (Eq. (five)) instead of Eqs. (2)–(4). Hither, the production of wealth is inversely proportional to the number of families in club if the chapters is exceeded (Eq. (9)), is proportional to the logarithm of labour and increases with linear feedback from wealth, and is perturbed past noise resulting from internal and environmental fluctuations post-obit a normal distribution (Eq. (x)). Finally, families produce offspring (Eq. (seven)) and strategy parameters are transmitted with slight mutation (Eq. (8)). The birth charge per unit increases linearly with wealth. Here, families reproduce without considering spousal relationship explicitly. The extended model with the marriage procedure is explained in Supplementary Text.
In the simulation, the initial values of strategies are s = 0.five and \(\lambda ={{\mathrm{log}}}\,two\) for all families. Hence, at the initial country, families tin form nuclear or extended families with equal probability, and the inheritance is moderately biased then that the share of the inheritance received past subsequent children is half of that received past the preceding children. In other words, the families are not differentiated as nuclear or extended, or as equal or strongly biased inheritance providers. However, no qualitative changes are observed under other initial conditions. The source lawmaking has been fabricated publicly bachelor in the Dataverse repository (Itao and Kaneko, 2021b), https://doi.org/ten.7910/DVN/3ZGCQI.
Results
Evolution of family systems
The simulations are performed for 2000 fourth dimension steps. The fourth dimension series of the evolution of family unit strategy parameters are shown in Fig. ii. Family strategies practice not diverge within each society, but are concentrated effectually a specific value adjusted to each given environmental status. The probability to form extended families southward (plotted in red) and the inequality in inheritance λ (plotted in blue) evolve depending on the values of land capacity c and wealth required for survival ϵ, respectively. The development of the strategy converges within ~1000 steps in every parameter region.
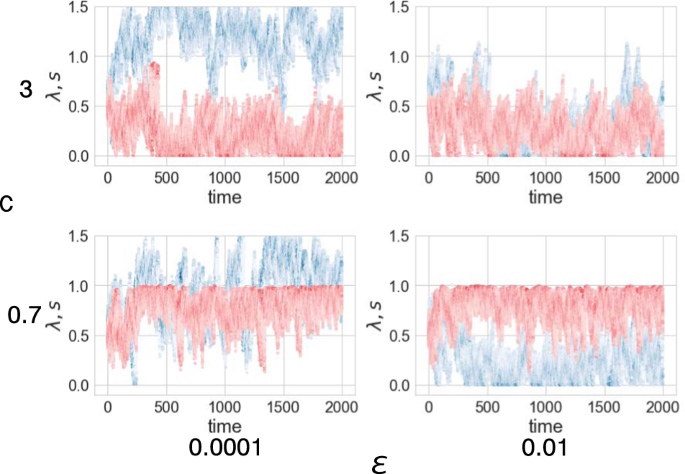
The temporal evolution of the values of the probability to form extended families due south (ruddy) and the inequality in inheritance λ (blue) of families in a society are plotted, for environmental weather condition with c = 0.seven, 3 and ϵ = 0.0001, 0.01.
Nosotros conducted multi-level evolutionary simulation 100 times for each condition and averaged the strategy parameters of families in the last m steps. Figure 3a, b show the dependence of s and λ on c and ϵ. Increasing land capacity c makes nuclear family strategies more preferable at both the family unit- and society-levels. Then, the probability of forming an extended family south decreases, implying the evolution of nuclear families. Increasing ϵ, the wealth required for survival, increases the demand for inheritance by younger siblings. This results in a smaller inequality in inheritance λ, indicating the evolution of the equal inheritance. Figure 3c shows the stage diagram of family systems. Here, nosotros classify the family systems equally extended if s ≥ 0.five, and as nuclear if s < 0.v. Similarly, we classify them as unequal inheritance sharers if \(\lambda \ge {{\mathrm{log}}}\,2\) and as equal if \(\lambda < {{\mathrm{log}}}\,2\). This criterion is determined according to whether the share of the inheritance awarded to the subsequent children is smaller (or larger) than half of that awarded to the preceding children. Therefore, the four bones family systems evolve depending on the 2 environmental parameters c and ϵ. A stalk family (plotted in greenish) evolves if c and ϵ are modest. A community family (plotted in orangish) evolves if c is small and ϵ is big. An absolute nuclear family (plotted in blue) evolves if c is large and ϵ is small, and an egalitarian nuclear family unit (plotted in yellowish) evolves if both c and ϵ are large.
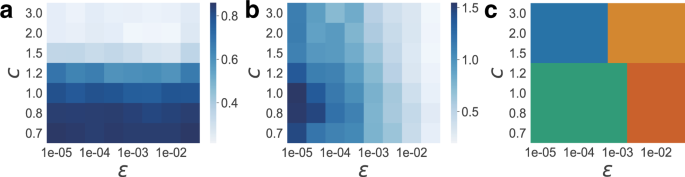
The graphs show the average values of family unit strategies (a, the probability to form extended families due south and b the inequality in inheritance λ) in the last 1000 steps of simulation. c Stage diagram of family systems. The environmental dependencies of stem (green), customs (orange), absolute nuclear (blue), and egalitarian nuclear (yellow) families are shown. Parent–child relationship for residence is classified every bit that of an extended family if s ≥ 0.v and every bit that of a nuclear family if s < 0.5. Inter-sibling relationship for inheritance is classified as unequal if \(\lambda \ \ge \ {{\mathrm{log}}}\,2\) and as equal if \(\lambda \ < \ {{\mathrm{log}}}\,two\).
We show the dependence of the phase diagrams of family systems upon other parameters in Figs. iv and S1. The phase diagrams plotted against c and ϵ are qualitatively robust and independent of the other parameter values. However, quantitative trends be. Generally, N due south and Due north f determine the strength of pick pressures at the family- and society-levels (Takeuchi et al., 2017; Traulsen and Nowak, 2006). For a large Northward f or small N southward (ultimately, if Northward due south = i), family unit-level competition becomes ascendant rather than social club-level competition, which leads to the development of selfish behaviour. Conversely, when society-level competition is dominant because of modest Due north f or large N s, cooperative behaviour evolves. Figure 4a, b show that, if N f is large or N s is small, nuclear families evolve fifty-fifty when c is small. Recall that the total production of siblings increases if they work independently, but that of society decreases because of the inefficiency in state usage if the capacity is limited. Therefore, choosing a nuclear family unit under small c is a selfish strategy that evolves for pocket-size N s and big Due north f. Equally wealth w accumulates, ϵ would become relatively minor for the wealth, and accumulation would be accelerated. All the same, when the minimal birth rate b is high, the number of offspring increases, and each share decreases. Therefore, less wealth is accumulated, and equal distribution evolves in larger parameter regions because of the relatively big ϵ, as shown in Fig. 4c. The dependence of the stage diagram on the parameters mutation charge per unit μ, decay of wealth d, and increase of birth rate past wealth f are shown in Fig. S1.
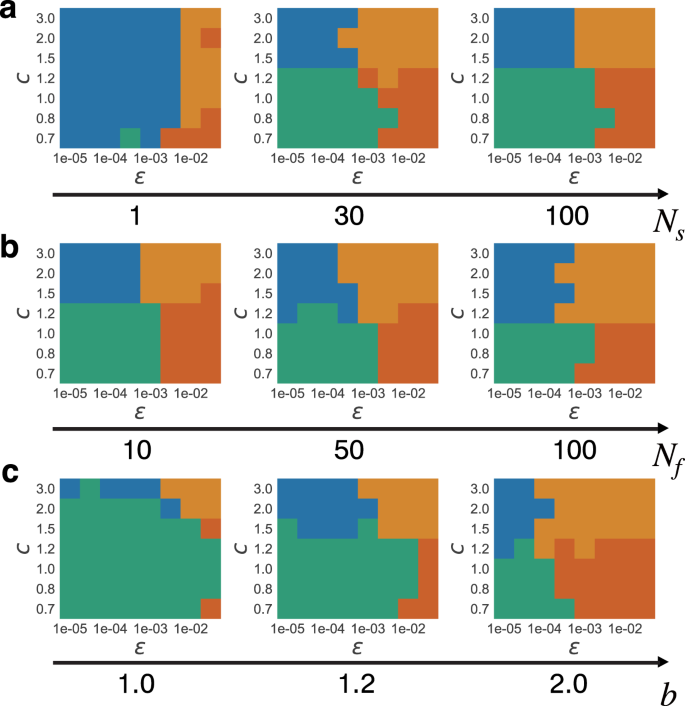
The graphs bear witness the dependence on parameters with * in Table ane (a the number of societies Ns, b the number of families Nf, c birth rate b). Unless the value is shown on the axis, the parameter values are fixed to those in Table 1.
Evolution of husband–married woman relationships in the extended model
The simulation results are shown in Fig. S2 for the extended model considering the marriage procedure. Parental investment is biased for sons about four times as much as daughters for virtually of the parameter regions. Investment for sons is advantageous because wealthy men can accept many wives and increase their fettle. Evolutionary anthropologists accept reported that girl-biased investment evolves under paternity uncertainty (Holden et al., 2003), which is beyond the telescopic of our model. Hence, information technology is reasonable that only son-biased investment evolves in our model.
Results also testify that the frequency of polygyny is <20%. The bias of parental investment and the frequency of polygyny are about contained of land capacity c or wealth required for survival ϵ. Furthermore, consideration of the marriage process just minimally affects the results for parent–kid and inter-sibling relationships. Hence, we will analyse the economic structures of evolved societies by using the previous minimal model in the following section.
Additionally, we studied a model in which the diminishing returns of family labour in production are relaxed, to consider labour-all-encompassing subsistence patterns other than agriculture. Figure S3 shows that if production increases linearly to the number of family labourers, the frequency of polygyny increases to more than than 20% almost independently of c and ϵ, even though the parental investment bias is almost the same as the to a higher place model. In this model, the increment in polygyny results from a larger fraction of relatively wealthy people. This scenario is consistent with empirical reports for foraging, horticultural and agropastoral societies (Ross et al., 2018). Extended families are dominant even when country capacity c is sufficient because they are no less preferable than nuclear families even at the family-level in this model. Withal, both nuclear and extended families are observed in most of the subsistence patterns (Murdock and White, 1969). It suggests that nuclear families can evolve attributable to some reasons not covered past our model. To discuss the variation of family systems depending on subsistence patterns, it will be necessary to consider the departure in productivity and lifestyle.
Wealth distribution and evolution of social structure
Subsequently, we investigated the wealth distribution of families for each gild after development. Notation that data from the wealth distribution in modern society suggest an exponential-type tail for the rich side (Chakrabarti et al., 2013; Tao et al., 2019) (say a log-normal (Gibrat, 1931) or gamma distribution (Chakraborti and Patriarca, 2008)), and a power distribution for the poor side (Reed, 2003) (say a gamma distribution (Chakraborti and Patriarca, 2008)). The gamma distribution is obtained by assuming the wealth growth with positive feedback and nonlinear saturation, as well as a multiplicative stochastic process, which are included in our model (see Supplementary Text).
Figure 5a shows the frequency distribution of the wealth of families within each lodge. In every parameter region, the distribution approximately follows a power-law on the poor side and has an exponential tail on the rich side, which is consistent with the to a higher place data. Because inherited wealth depends on birth gild, we likewise plotted the distributions of wealth past distinguishing the eldest siblings from the others in Fig. 5b. With decreasing wealth required for survival ϵ, and consequently increasing inheritance inequality, the distributions of the wealth of siblings divide further. As a event, the accumulation of wealth by heirs is accelerated. Decreasing country chapters c and the evolution of extended families result in poorer younger siblings, whereas greater country capacity c and the evolution of nuclear families requite rise to wealthier younger siblings.
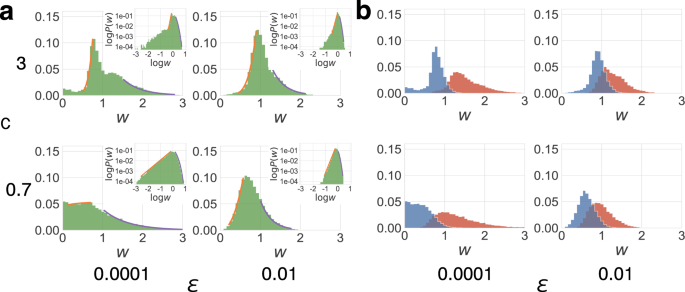
a The graphs testify the frequency distribution of family unit wealth in the terminal 1000 steps for environmental conditions with c = 0.7, iii and ϵ = 0.0001, 0.01. The orangish line shows the power-law fitting, and the purple line shows the exponential distribution fitting. The insets show the log–log plot of the frequency distribution. b The wealth distribution of the eldest (crimson) and younger siblings (blue).
Although the wealth distribution follows the power-law w α on the poor side and the exponential distribution \(\exp (-\beta westward)\) on the rich side universally, the heaviness of tails depends on the ecology parameters. We fitted values for the lightness of the poor tail α and those for the rich tail β and averaged them over 100 trials for each environmental parameter c and ϵ in Fig. 6a, b, respectively. Smaller c results in smaller α, i.eastward. the heavier tail is on the poor side, while smaller ϵ results in smaller β, i.e. the heavier tail is on the rich side. These results advise the characteristics of the wealth distribution in the iv respective family systems. However, it remains unclear whether they outcome from environmental atmospheric condition or family systems. To ostend the relevance of family systems, we computed the dependence of wealth distributions on family systems past sampling each family system using fixed environmental parameters almost the boundary of the four phases of family unit systems, where the values of southward and λ are distributed to encompass all iv family unit systems.
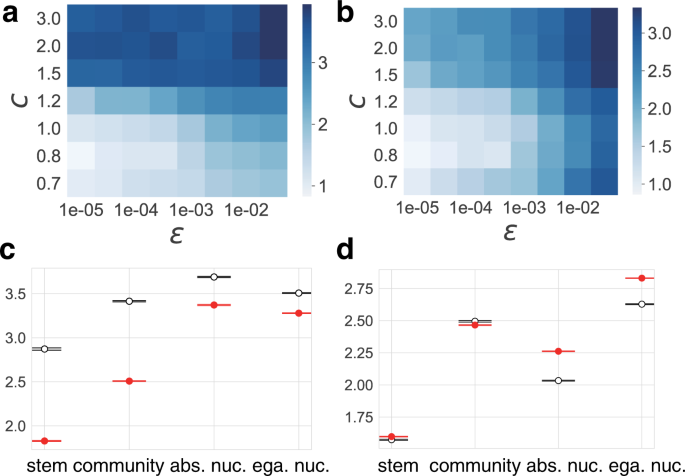
a Lightness of the poor tail α given by the power-law plumbing equipment w α . b Lightness of the rich tail β given by the exponential fitting \(\exp (-\beta w)\). Smaller α and β show heavier tails for the poor and rich sides, respectively. c, d Averaged value of α (c) and β (d) classified by the dominant family system (stem, community, absolute nuclear, and egalitarian nuclear families) in each club, with error bars. Values for the ecology parameters fixed to ϵ = 0.0003 and c = one.5 are plotted in black, whereas those averaged over ϵ = 0.0001, 0.0003, 0.001, 0.003 and c = 1.0, 1.ii, i.5, two.0 are plotted in ruddy.
The boilerplate values of α and β for each family system, which were sampled for the fixed environmental parameters (plotted in blackness), are shown in Fig. 6c, d. They demonstrate the trend that the poor tail is heavier for extended families with poor younger siblings, whereas the rich tail is heavier for unequal inheritance with rich heirs. By comparing these results with the results averaged over several ecology parameters around the phase purlieus (plotted in ruby-red), information technology is shown that the above tendency depends on each family organisation, and is farther intensified past environmental parameter values.
Empirical data analyses
Next, nosotros verify our results on the relationship between environmental conditions, family systems, and economic structures. Using the global ethnographic database of 186 premodern societies, called SCCS (Kirby et al., 2016; Murdock and White, 1969), empirical data analyses were conducted.
First, we classified family systems of pre-industrial agricultural societies. We so identified pre-industrial agricultural societies by using the Subsistence economy: ascendant activeness variables (5–vii correspond to agriculture). Then, we identified the family systems past using Domestic organisation (one–five correspond to nuclear families and six–8 correspond to extended families) and Inheritance distribution for movable property (1 corresponds to equal and ii–4 correspond to strongly biased inheritance) (see Supplementary Tables for a detailed explanation of these variables). Out of 186 societies in SCCS, 91 societies conducted agriculture and inheritance of movable properties. Among them, 14 societies were classified equally stem families, 30 as community families, 17 as absolute nuclear families, and 30 every bit egalitarian nuclear families. Figure S4 shows their geographic distribution. Hither, we used the data on the inheritance of movable backdrop to identify inter-sibling relationships. Nonetheless, like trends on the following variables were accomplished, fifty-fifty when we used those pertaining to the inheritance of real holding, as shown in Table S2.
Adjacent, nosotros conducted Spearman's rank correlation analyses and calculated the correlation between SCCS variables and parent–child (nuclear or extended) or inter-sibling (strongly biased or equal) relationships. The database contains various variables of socio-ecological factors. By calculating the correlation for each variable and listing the variables in descending order in the accented value of the correlation, we found those variables related to the parameters in our model in the top of the list. The variables that are highly correlated with parent–child and inter-sibling relationships are listed in Tabular array S1 and Table S2, respectively. Among them, we bear witness the variables that can be related to the model parameters in Tabular array 2.
Table ii shows the dependence of family unit systems on environmental weather condition. Communality of land and Land Shortage, suggesting larger and smaller land capacity c, respectively, are correlated with extended families (Corr. −0.31 (P = 0.03) and Corr. 0.26 (P = 0.09), respectively). This is consistent with the theoretical results showing the evolution of extended families for smaller c. On the other manus, Frequency of internal warfare and Acceptability of violence within order suggest that fierce conflict is more frequently observed in societies with equal inheritance (Corr. 0.36 (P = 0.08) and Corr. 0.27 (P = 0.13), respectively). Such violence volition harm goods and require families to accept more wealth to survive; as a result, the wealth required for survival ϵ increases in our model. Accordingly, equal inheritance is more than frequent for larger ϵ, equally is consistent with our results.
Furthermore, the data suggest the correlation between family systems and economic structures. Number of poor implying smaller α is positively correlated with extended families (Corr. 0.29 (P = 0.06)), whereas Number of rich people implying smaller β is negatively correlated with equal inheritance (Corr. −0.37 (P = 0.01)). Thus, the empirical data are consequent with our simulation results, concerning the relationship between environmental atmospheric condition, family systems, and society-level economic structures. See Supplementary Tables for the explanation on values of SCCS variables.
Discussion
By simulating the multi-level evolution model of family unit systems, we demonstrated the evolution of family systems depending on the environmental parameters for the capacity of available land resources c and the amount of wealth required for a family unit to survive ϵ. As for parent–kid relationships, if there is sufficient land chapters, nuclear families evolve, whereas extended families evolve under a state shortage. As for inter-sibling relationships, if the wealth required for survival is large, equal inheritance evolves, whereas strongly biased inheritance evolves when that is small. Therefore, the iv basic family systems characterised by both relationships above are represented as 'phases' depending on c and ϵ. Past considering marriage, nosotros and so confirmed son-biased investment and infrequent polygyny. Additionally, we clarified the characteristics of wealth distribution determined by the dominant family systems within societies. The tail of the poor side is heavier (that is, many poor people) for extended families, and that of the rich side is heavier (that is, many rich people) for families with diff inheritance. Empirical data analyses of premodern societies in SCCS supported our results.
Now, we refer to demographics and socioeconomic histories in the premodern and modernising era, especially in Western Europe and Eastern asia. The country capacity c in our model can be measured approximately by the period since the onset of agriculture. In the areas where agriculture started early on, population growth resulted in the exhaustion of available country, and labour-intensive farming developed, as observed in China (Pomeranz, 2000; Wallerstein, 2011), Russia (Hizen, 1994), and Nihon (Hayami, 2015). In Western Europe, especially Holland, the Paris Bowl, Southern England, and Key Spain, the capacity was large until industrialisation, and labour-saving farming was developed (Pomeranz, 2000) equally a effect of the following reasons: agricultural progress in medieval times enabled virgin land cultivation by gathering the children not inheriting the parental lands (Bacci, 2017; Cameron et al., 1993; Grigg, 1980; Pirenne, 1956); the population stagnated in premodern times because of religious wars and plagues (Bacci, 2017); and colonies were established early on (Wallerstein, 2011). Accordingly, the model result apropos c implies that extended families evolve in the areas where agriculture started early. Tabular array 2 likewise suggests that the exhaustion of land leads to the development of extended families.
As for wealth required for survival ϵ, demographics report that the frequency of violent conflict decreased in the following society in Eurasia: the centre of the continent, peripheral, and island regions (Khazanov and Wink, 2012; Macfarlane, 2002; Umesao, 2003). The regions close to the pole of civilisation and/or those frequently attacked by foreign people would take a big ϵ. Hence, the model result concerning ϵ implies that equal inheritance is dominant in the centre of the Eurasia continent and other regions that are vulnerable to warfare (see Fig. S4). The results of the empirical data analysis in Table 2 also support the correlation between such violent disharmonize with the evolution of equal inheritance.
From geohistorical reports discussed to a higher place, the family systems in each region can exist explained: absolute nuclear families (nuclear family, unequal inheritance) in England and the Netherlands, where available land resources were sufficient and wealth required for survival was pocket-sized; egalitarian nuclear families (nuclear family, equal inheritance) in French republic, Spain, and Italy, where both land capacity and necessity of wealth were large; stem families (extended family, diff inheritance) in Japan, Deutschland and many parts of rural Western Europe, where both of them were minor; and customs families (extended family, equal inheritance) in Red china, Russia, and Northern Republic of india, where state chapters was small and necessity of wealth was big (Berkner, 1972; Todd, 2011).
Autonomously from these ecology conditions, the number of families within a society N f, the number of competing societies N s, and birth charge per unit b are also relevant parameters for determining the family system. N f is large for big-calibration land management as seen in England, holland, France, and Spain, whereas N f is small-scale and Northward s is large in family unit farm management as observed in Cathay, Russia, Japan, and Germany (Bacci, 2017; Cameron et al., 1993; Hizen, 1994; Pomeranz, 2000; Wallerstein, 2011). The trends in Fig. 4a, b are consistent with the observation of nuclear families in the onetime regions and extended families in the latter. The birth rates were low in Japan and Western Europe, especially in England (Macfarlane, 2002), and higher in Russian federation (Hizen, 1994). The observation of unequal inheritance in the former regions and equal inheritance in the latter demonstrates a similar tendency to Fig. 4c.
Next, nosotros examine the validity of our results regarding the relationships betwixt family systems, socio-economic structures, and modern social ideologies. Effigy half-dozen suggests that, in England and holland involving accented nuclear families, the tail of wealth distribution is heavy on the rich side and light on the poor side. Indeed, wealthy farmers prospered and employed a majority every bit labourers who had better living standards than those in poorer regions (Laslett, 2015; Macfarlane, 2002; Shaw-Taylor, 2012; Tawney, 1912; Todd, 1990; Wallerstein, 2011). The accumulation of majuscule and independent labour forces explains the development of individual freedom and capitalism in England (Braudel, 1992a, b, c; Todd, 1990; Wallerstein, 2011). Wealth distribution in French republic and Spain, involving egalitarian nuclear families, was suggested to have lite tails on both the rich and poor sides. That is, agricultural societies were less differentiated and weakly stratified (Dupeux, 1972; Rösener, 1993; Wallerstein, 2011), which forms the footing of the values of liberty and equality. Our results suggest that wealth distribution in Frg, Sweden, and Japan, involving stem families, had heavy tails on both rich and poor sides. Wealthy farmers prospered past exploiting others and the stratification of guild advanced in accord with the order and course distinctions (Hayami, 2015; Hayami and Kurosu, 2001; Kastner, 1978; Mager, 1981; Rösener, 1993; Todd, 1990). Wealth distribution in Russia and China, involving community families, was suggested to have a low-cal rich tail and a heavy poor tail. Indeed, the middle class was significantly thin, and people were uniformly poor (Rösener, 1993), which led to the adoption of communism (Thaxton, 1997; Weber, 1995). In this manner, the wealth distribution obtained in our model connects family systems with order-level characteristics observed in socio-economic history. A report of political ideology showed that people supported authoritarianism in the presence of many individuals being exposed to threats, and egalitarianism in the absenteeism of strong inequality or power imbalance (Claessens et al., 2020). Our results are consistent with this, because the heavier poor and rich tails imply the presence of vulnerable and privileged people, respectively.
Notation that our results regarding the family systems and the socio-economical structures are expected to be rather full general. The conclusion here is independent of the details of the present model, as long equally the production increases sub-linearly with labour input, and multi-level selection of families and societies is considered.
Ane can also hash out long-term changes in land capacity c and wealth required for survival ϵ, and their influence on family unit systems. At times of cultivation, a nuclear family unit evolves because of sufficient capacity. As the population increases and chapters becomes limited, an extended family unit would replace it. Additionally, considering of the dense population, the risks of invasion from surrounding areas and conflict inside societies increase, and accordingly, owing to the loss of wealth past violence, ϵ would increase gradually. This scenario explains the historical change of family systems from a nuclear family unit to a stem family unit, and and then to a community family (Todd, 2011).
Environmental factors alter gradually owing to the interaction between society and the environment. Even so, the change in ecology factors, in turn, will alter family systems and social structures. Such historical dynamics have been discussed as the interaction of factors on different time scales (Braudel, 1992a, b, c). To hash out such interaction of factors at different levels, the present constructive model volition give a basic explanation.
The present model has some limitations. First, the differentiation of people between the elite and the majority was not considered. As society becomes stratified, people start to rent land from the aristocracy. This results in the departure of ecology factors and family unit systems between them (Todd, 2011). A model is needed for handling social stratification and the interaction of classes to talk over broader issues. Second, we did not model intra-family contest for resources explicitly and the relationships between family systems and such competition remain unsolved. Intra-family competition has attracted attention in evolutionary anthropology (Ji et al., 2014; Trivers, 1974). In fact, the previous studies have revealed the high condition of the elderly in extended families (Lee and Kezis, 1979), and sibling competition over the land inheritance (Gibson and Gurmu, 2011). The model, then, needs to have three levels, i.e. individual, family, and society. Finally, the electric current model focuses only on pre-industrial agricultural societies. Models focusing on other subsistence patterns are needed to hash out the diversity of family systems widely. For example, Fig. S3 shows that if the diminishing returns of family unit labour are relaxed, the frequency of polygyny increases. Furthermore, in the modern world, agricultural societies should no longer be regarded as isolated systems, but constitute components of a world-system (Wallerstein, 2011). A new model needs to be developed to consider the interaction between towns and agricultural societies, too as international, political, and commercial networks.
Furthermore, the present empirical information analyses have some limitations. Outset, nosotros could only analyse the correlation between cultural variables and family systems. Although information technology is desirable to conduct better analyses (such as classification learning) to reveal features relevant to family systems, it was infeasible due to data insufficiency. In this study, we used SCCS in which the data for a variety of socio-ecological factors are available. SCCS enabled u.s. to examination the correlation betwixt model parameters and family systems empirically, although the sample size was express. Future works should make use of other databases that include more societies (but fewer variables per order), such as the Ethnographic Atlas (Murdock, 1967). 2d, nosotros could not analyse causal relationships owing to a lack of chronological data. Our correlation analyses are insufficient to examine whether history progresses equally our model predicted.
Here, the collaboration of field studies, historical analyses, and theoretical modelling is necessary to further elucidate the historical dynamics of societies. Field studies draw the individual- or family-level behaviour and lodge-level structures synchronically. Historical or phylogenetic analyses unveil the diachronic change of such factors. In addition, Leach has emphasised the importance of generalising ethnographic findings by using mathematical formulation to unveil universal structural patterns that may appear in any type of lodge (Leach, 1961). The constructive model, every bit presented here, provides a simplified mathematical expression of family unit behaviours, gives a general framework that allows comparison of various societies, explains the universal patterns between family- and lodge-level factors, and reveals their historical evolution.
To summarise, we presented a multi-level evolution model to account for the emergence of the four basic family systems and the resultant socio-economic structures depending on environmental atmospheric condition, as is consistent with family unit-level anthropological studies and society-level economic histories. Hither, the microscopic characteristics of families determine the macroscopic economic structures, which forms the footing for the development of societies. This report allows an explanation of the universal evolutionary constraint that homo societies satisfy.
Data availability
The source code has been made publicly available in the Dataverse repository (Itao and Kaneko, 2021b), https://doi.org/10.7910/DVN/3ZGCQI, or https://github.com/KenjiItao/family_system.git.
References
-
Bacci ML (2017) A concise history of world population. John Wiley & Sons
-
Berkner LK (1972) The stem family unit and the developmental wheel of the peasant household: An eighteenth-century austrian case. Am Hist Rev 77(2):398–418
-
Berkner LK (1976) Inheritance, land tenure and peasant family structure: a German regional comparison in family and inheritance. In: Goody JR, Thirsk J, Thompson EP (eds) Rural Society in Western Europe 1200–1800. Cambridge University Press
-
Braudel F (1992a) Civilization and capitalism, 15th–18th century, vol I: The structure of everyday life. University of California Press
-
Braudel F (1992b) Civilisation and capitalism, 15th-18th century, vol. Ii: The wheels of commerce. University of California Printing
-
Braudel F (1992c) Civilization and capitalism, 15th–18th century, vol. 3: The perspective of the world. University of California Press
-
Cameron RE et al. (1993) A concise economic history of the earth: from Paleolithic times to the present. Oxford University Press, USA
-
Cavalli-Sforza LL, Feldman MW (1981) Cultural transmission and evolution: a quantitative approach. Princeton Academy Press
-
Chakrabarti BK, Chakraborti A, Chakravarty SR, Chatterjee A (2013). Econophysics of income and wealth distributions. Cambridge University Press
-
Chakraborti A, Patriarca Chiliad (2008) Gamma-distribution and wealth inequality. Pramana 71(2):233–243
-
Claessens S, Fischer Thousand, Chaudhuri A, Sibley C. GAtkinson Q. D, The dual evolutionary foundations of political ideology Nat Hum Behav iv:33 6–345
-
Colleran, H. (2014). Farming in transition: land and property inheritance in a rural Smoothen population. Soc. Biol. Hum. Aff, 78(1&2): 7–nineteen
-
Creanza N, Kolodny O, Feldman MW (2017) Cultural evolutionary theory: How culture evolves and why information technology matters. Proc Natl Acad Sci USA 114(30):7782–7789
-
Dupeux G (1972) La société française, 1789–1970. FeniXX
-
Evenson RE, Mwabu G (2001) The effect of agronomical extension on farm yields in kenya. Afr Dev Rev xiii(1):ane–23
-
Fortunato Fifty, Jordan F (2010) Your identify or mine? a phylogenetic comparative analysis of marital residence in indo-european and austronesian societies. Philos Trans R Soc B: Biol Sci 365(1559):3913–3922
-
Fortunato 50, Holden C, Mace R (2006) From bridewealth to dowry? Human Nature 17(4):355–376
-
Flim-flam R (1983) Kinship and spousal relationship: An anthropological perspective, vol 50. Cambridge University Press
-
Gibrat R (1931). Les inégalits économiques. Librairie du Recueil Sirey, Paris
-
Gibson MA, Gurmu E (2011) Land inheritance establishes sibling competition for wedlock and reproduction in rural ethiopia. Proc Natl Acad Sci United states of america 108(6):2200–2204
-
Goldschmidt W, Kunkel EJ (1971) The structure of the peasant family. Am Anthropol 73(5):1058–1076
-
Grigg DB (1980) Population growth and agrarian alter: an historical perspective. Loving cup Annal
-
Guglielmino CR, Viganotti C, Hewlett B, Cavalli-Sforza LL (1995) Cultural variation in africa: role of mechanisms of manual and accommodation. Proc Natl Acad Sci USA 92(16):7585–7589
-
Harrell S (1997) Human Families. Westview Press
-
Hayami A (2015) Nippon's Industrious Revolution: Economical and Social Transformations in the Early Modernistic Period. Springer
-
Hayami A, Kurosu S (2001) Regional diversity in demographic and family patterns in preindustrial japan. J Jpn Stud 27:295–321
-
Hizen East (1994) The demographic background of the land problem in Russia (1880's–1920'south). Jpn Slav East Eur Stud fifteen:1–25
-
Holden CJ, Mace R (2003) Spread of cattle led to the loss of matrilineal descent in africa: a coevolutionary analysis. Proc R Soc Lond Ser B: Biol Sci 270(1532):2425–2433
-
Holden CJ, Sear R, Mace R (2003) Matriliny as daughter-biased investment. Evol Hum Behav 24(2):99–112
-
Itao K, Kaneko K (2020) Evolution of kinship structures driven by marriage necktie and contest. Proc Natl Acad Sci USA 117(5):2378–2384
-
Itao K, Kaneko K (2021a) Emergence of kinship structures and descent systems: multi-level evolutionary simulation and empirical data analyses. Preprint at arXiv:2105.08014
-
Itao K, Kaneko K (2021b) Replication Data for: Kenji Itao and Kunihiko Kaneko "Evolution of family systems and resultant socio-economic structures". https://doi.org/10.7910/DVN/3ZGCQI
-
Ji T, Xu J-J, Mace R (2014) Intergenerational and sibling conflict under patrilocality. Hum Nat 25(i):66–79
-
Kaser K (2002) Power and inheritance: male domination, property, and family in eastern europe, 1500–1900. Hist Fam 7(3):375–395
-
Kastner K (1978) Aus der Chronik des Kirchspiels Hohenkirch Kr [eis] Briesen (Westpr [eussen]).: Seine Landgemeinden und Gutsbezirke. Truso-Verlag
-
Khazanov A, Wink A (2012). Nomads in the sedentary world. Taylor & Francis
-
Kirby KR, Gray RD, Greenhill SJ, Hashemite kingdom of jordan FM, Gomes-Ng S, Bibiko H-J, Blasi DE, Botero CA, Bowern C, Ember CR et al. (2016) D-place: a global database of cultural, linguistic and environmental diversity. PLoS I 11(7):e0158391
-
Laslett P (1988) Family unit, kinship and collectivity equally systems of support in pre-industrial europe: a consideration of the 'nuclear-hardship'hypothesis. Contin Change iii(2):153–175
-
Laslett P (2015) The world we have lost: farther explored. Routledge
-
Leach ER (1961) Rethinking anthropology, london: athlone, london school of economics and political scientific discipline. Monogr Soc Anthropol
-
Lee GR, Kezis Chiliad (1979) Family structure and the status of the elderly: a preliminary empirical study. J Comp Fam Stud x(3):429–443
-
Lévi-Strauss C (1958). Anthropologie structurale. Plon, Paris
-
Mace R, Jordan FM (2011) Macro-evolutionary studies of cultural diverseness: a review of empirical studies of cultural transmission and cultural accommodation. Philos Trans R Soc B: Biol Sci 366(1563):402–411
-
Macfarlan SJ, Quinlan RJ, Mail Eastward (2019) Emergent matriliny in a matrifocal, patrilineal population: a male person coalitionary perspective. Philos Trans R Soc B 374(1780):20180073
-
Macfarlane A (2002) The savage wars of peace: England, Nihon and the Malthusian trap. Springer
-
Mager W (1981) Haushalt und Familie in protoindustrieller Gesellschaft: Spenge (Ravensberg) während der ersten Hälfte des 19. Jahrhunderts. Eine Fallstudie
-
Malthus TR (1798) An essay on the principle of population as it affects the future improvement of society, with remarks on the speculations of Mr/ Godwin, M. Condorcet, and other writers. J. Johnson, London
-
Minocher R, Duda P, Jaeggi AV (2019) Explaining marriage patterns in a globally representative sample through socio-ecology and population history: a bayesian phylogenetic analysis using a new supertree. Evol Hum Behav 40(2):176–187
-
Mulder MB, George-Cramer M, Eshleman J, Ortolani A (2001) A study of eastward african kinship and matrimony using a phylogenetically based comparative method. Am Anthropol 103(4):1059–1082
-
Murdock GP (1967) Ethnographic atlas: a summary. Ethnology half-dozen(2):109–236
-
Murdock GP, White DR (1969) Standard cross-cultural sample. Ethnology 8(4):329–369
-
Pirenne H (1956) Economical and social history of medieval Europe, vol 60. Houghton Mifflin Harcourt
-
Pomeranz Thou (2000) The not bad departure: Red china, Europe, and the making of the mod globe economic system. Princeton University Press
-
Reed WJ (2003) The pareto law of incomes-an explanation and an extension. Physica A 319:469–486
-
Ricardo D (1891) Principles of political economy and revenue enhancement. G. Bong and sons
-
Rösener West (1993) Die Bauern in der europäischen Geschichte. CH Beck
-
Ross CT, Borgerhoff Mulder Thou, Oh Southward-Y, Bowles S, Beheim B, Bunce J, Caudell M, Clark Yard, Colleran H, Cortez C et al. (2018) Greater wealth inequality, less polygyny: rethinking the polygyny threshold model. J R Soc Interface 15(144):20180035
-
Schulz, J. F., Bahrami-Rad, D., Beauchamp, J. P. & Henrich, J. (2019) The Church, intensive kinship, and global psychological variation. Science 366:eaau5141
-
Shaw-Taylor L (2012) The rise of agrestal capitalism and the refuse of family farming in england 1. Econ Hist Rev 65(1):26–threescore
-
Shenk MK, Mattison SM (2011) The rebirth of kinship. Hum Nat 22(1):1–15
-
Spencer CS, Redmond EM (2001) Multilevel selection and political development in the valley of oaxaca, 500–100 bc. J Anthropol Archaeol 20(2):195–229
-
Takeuchi N, Hogeweg P, Kaneko K (2017) The origin of a primordial genome through spontaneous symmetry breaking. Nat Commun viii(1):one–xi
-
Tao Y, Wu Ten, Zhou T, Yan W, Huang Y, Yu H, Mondal B, Yakovenko VM (2019) Exponential structure of income inequality: bear witness from 67 countries. J Econ Collaborate Coord fourteen(2):345–376
-
Tawney RH (1912) The agrestal problem in the sixteenth century. Longmans, Light-green and Company
-
Thaxton R (1997) Salt of the earth: The political origins of peasant protestation and communist revolution in China. University of California Press
-
Todd East (1990) 50'invention de l'Europe. Editions du Seuil Paris
-
Todd Due east (1999) La diversité du monde: structures familales et modernité. Seuil
-
Todd E (2011) L'origine des systèmes familiaux, vol 1. Gallimard Paris
-
Traulsen A, Nowak MA (2006) Evolution of cooperation by multilevel pick. Proc Natl Acad Sci USA 103(29):10952–10955
-
Trivers RL (1974) Parent–offspring conflict. Integr Comp Biol fourteen(ane):249–264
-
Turchin P, Gavrilets South (2009) Development of complex hierarchical societies. Soc Evol Hist 8(two):167–198
-
Umesao T (2003) An ecological view of history: Japanese civilization in the globe context. ISBS
-
Wallerstein I (2011) The modernistic earth-organisation I: Capitalist agronomics and the origins of the European earth-economic system in the sixteenth century, vol ane. University of California Printing
-
Weber M (1995) The Russian Revolutions. Cornell Academy Press
-
White HC (1963) An beefcake of kinship: mathematical models for structures of cumulated roles. Prentice-Hall
-
Wilson DS (1997) Altruism and organism: disentangling the themes of multilevel pick theory. Am Nat 150(1):122–S134
-
Wilson DS, Wilson EO (2007) Rethinking the theoretical foundation of sociobiology. Q Rev Biol 82(4):327–348
Acknowledgements
The authors thank Tetsuhiro Southward. Hatakeyama, Yuma Fujimoto, and Kenji Okubo for a stimulating give-and-take, and Yasuo Ihara for illuminating comments. This study was partially supported by a Grant-in-Help for Scientific Research on Innovative Areas (17H06386) from the Ministry building of Education, Civilisation, Sports, Science, and Technology (MEXT) of Japan.
Author data
Affiliations
Respective author
Ethics declarations
Competing interests
The authors declare no competing interests.
Boosted information
Publisher'south annotation Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This commodity is licensed under a Artistic Commons Attribution 4.0 International License, which permits apply, sharing, adaptation, distribution and reproduction in any medium or format, every bit long every bit you requite advisable credit to the original author(due south) and the source, provide a link to the Artistic Commons license, and indicate if changes were made. The images or other tertiary party fabric in this article are included in the article's Artistic Eatables license, unless indicated otherwise in a credit line to the material. If material is non included in the article'southward Creative Commons license and your intended utilise is not permitted by statutory regulation or exceeds the permitted utilize, you will need to obtain permission direct from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/four.0/.
Reprints and Permissions
About this article
Cite this article
Itao, K., Kaneko, K. Evolution of family systems and resultant socio-economic structures. Humanit Soc Sci Commun 8, 243 (2021). https://doi.org/10.1057/s41599-021-00919-two
-
Received:
-
Accustomed:
-
Published:
-
DOI : https://doi.org/ten.1057/s41599-021-00919-2
Source: https://www.nature.com/articles/s41599-021-00919-2
0 Response to "How Do Families Adapt to Social Changes and Economic Development"
Post a Comment